With microtonal music the sound of intervals and chords can be more or less dissonant or alien-sounding. Partly this is due to us being used to hearning acoustic music in 12-TET, with timbres that almost without exception share the same harmonic series. The acronym stands for twelve tone equal temperament, where each octave is divided into twelve equal steps. The temperament has has dominated western music for the last hundred years or so. Before that all music was in practice tempered some way, to make chords and intervals more consonant for any given peformance.
Let’s venture deeper into the territory though, and look at the effect the harmonic series has on different tunings and scales. We shall construct a completely novel harmonic series based on the golden ratio instead of the usual integral series. We will also adapt our tuning so that the new timbre can be played consonantly. It will sound like this:
Download the project from here, if you just want to hear the sounds or use the additive synth.
About terminology:
Xenharmonic = “Every sound has an internal structure that determines its tone quality or timbre. When the larger structure of the music (the musical scale) reflects this internal structure, then the timbre and the tuning are related in a fundamental way. Music made with such related timbres and tunings is called xentonal. “(https://sethares.engr.wisc.edu/xentone.html)
The harmonic series that most physical instruments and the human voice produce, lines up nicely with 12-TET. Between simultaneous notes the sound is generally consonant, although some beating is evident because most intervals are a bit out of tune between each other. This is another topic, about which there’s lots of information readily available already, if you want to get into the details.
One solution is to use a so called just tuning, where every interval is perfect. For example’s sake, here’s are the first partials of a just C major triad in just tuning:
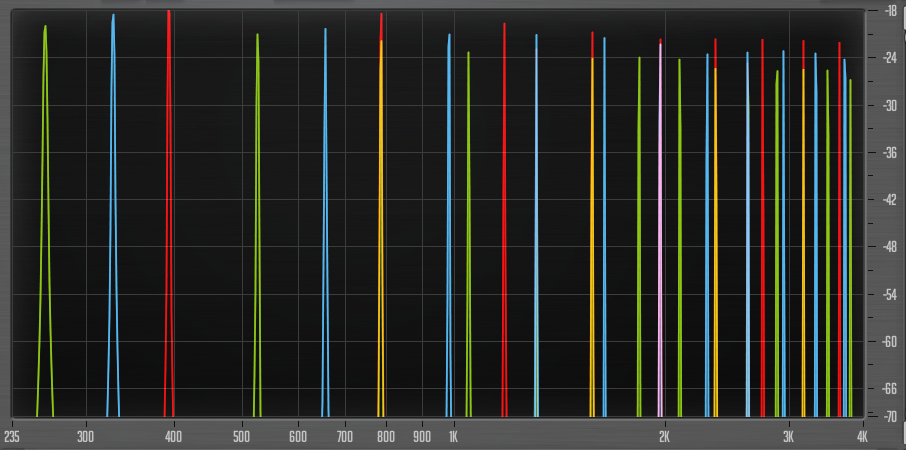
You see here first the fundamentals, spread out as expected, then the second partial of C, at an octave, then the second partial of E, and after that a yellow partial. That is actually the third partial of C coinciding with the second partial of G. And so on. The sound is very even and harmonic. Especially the fifth has many partials lining up with those of the octaves (2,3,6,9, etc). It can be argued that just tuning is close to optimal regarding dissonance with 12-TET. Problems arise though when transposing, because the different steps are not of an equal size, and this is the reason 12-TET is widely used these days (along with everybody just being used to it).
A harmonic series is simply a repeating series of sinewaves, in the usual case integral multiples of the base frequency. So for a note at 440 hz the harmonic series is formed by vibrations at 440hz, 880hz, 1320hz, 1760hz and so on. Except for struck metal pieces and non-uniform (ever drop some superglue on a guitar string and see how it sounds after that?) strings basically every instrument we’ve ever heard creates this same series. The unique sound of each instrument emerges from the relative amplitude and pitch modulation envelopes of each partial.
But what happens when we use a tuning other than 12-TET? Or a sound with a different harmonic series? Why does such music often sound a bit agitated and even unpleasant to many people?
First, a few words about perceived consonance and dissonance. Basically, when two vibrations are playing within a certain distance between each other, most people perceive a dissonant sensation. All instrument sounds are made up from several sine waves, often dozens or even hundreds, depending on how bright the sound is. It is inevitable than when playing music with such sounds a lot of them are going to be stacked more or less closely together.
If you’re interested in more details, search for information about “critical bands” in human hearing. The book “Tuning, Timbre, Spectrum, Scale” by William Sethares has also a great chapter on the matter. Basically the reason behind the sensation of dissonance is related to how sound vibrates along the basilar membrane inside the ear canal, along with some psychoacoustic phenomena. Imagine a point vibrating on a flexible substance: it will always necessarily drag along some nearby material.
For frequencies below 500hz the width of one critical band is around 100hz, and they get progressively wider with higher frequencies, with a width of 2500hz at 10khz.
In short, when several sinewaves are heard simultaneously, their pitches can be perceived as separate only if the difference in frequency is more than the width of the critical band they are occupying. So if two sinewaves at 500hz and 530hz are played simultaneously, they can’t be perceived as discrete tones, and a combination tone is heard instead.
The combination tones will have beating at the frequency of the difference in hz between the two waves (yes, even if the waves are played via headphones to different ears, so the beating phenomenon is not purely physical).
For sinewaves of 400 and 410hz you won’t hear two sinewaves, but instead one wave beating at 10hz. With small differences the beating is clearly perceptible, and eventually as the difference grows, the second tone starts to emerge individually. Between the beating and separation there is a region of dissonance. This dissonance is at it’s maximum around the frequency difference of one quarter the width of the critical band.
So for three waves at 275hz, 300hz, and 325hz we will have the most dissonant combination sound possible (on average, these number are empirical averages from research). The width of a critical band is around 100hz for a 300hz tone.
When looking at timbres and scales, the goal is to avoid partials that have a distance of about the quarter of the width of the critical band between them, when the scale is played. Here is a helpful table I borrowed from the Internet (nevermind that “bark” thing, it’s just what they’re called sometimes):
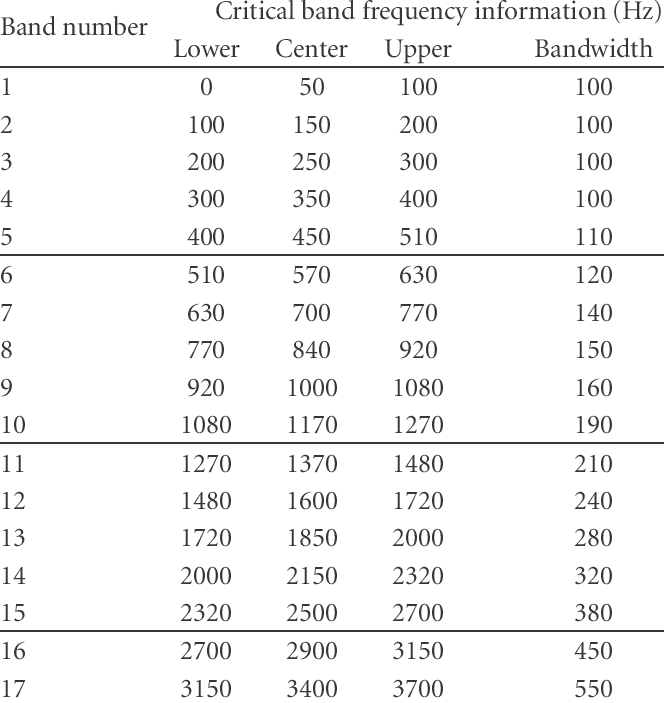
That’s it for the theory. For more details, I really, really recommend the book by Sethares. There is a study group in Facebook, where you can download the book. Notice that technically this is illegal, if you can afford the price of around 100€, I recommend buying the book and supporting the author.
Now back to our task of creating a new harmomic series.
Additive synthesis is a good way to achieve our goal, since it allows the free placement of each partial.
I have created an additive oscillator with 48 partials in the Grid. It is quite CPU heavy, so what I do is set it to something around 3-7 voices when working with the patch, and then increasing the amount of voices during rendering.
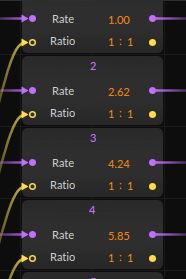
First, we need to calculate partial ratios for our new series. Below is a table showing all of them (you can enter floating point numbers with a lot of decimals and Bitwig will use the actual value, altough it will always show only two.):
| 1 | 1,000000 | 17 | 26,888544 | 33 | 52,777088 |
| 2 | 2,618034 | 18 | 28,506578 | 34 | 54,395122 |
| 3 | 4,236068 | 19 | 30,124612 | 35 | 56,013156 |
| 4 | 5,854102 | 20 | 31,742646 | 36 | 57,631190 |
| 5 | 7,472136 | 21 | 33,360680 | 37 | 59,249224 |
| 6 | 9,090170 | 22 | 34,978714 | 38 | 60,867258 |
| 7 | 10,708204 | 23 | 36,596748 | 39 | 62,485292 |
| 8 | 12,326238 | 24 | 38,214782 | 40 | 64,103326 |
| 9 | 13,944272 | 25 | 39,832816 | 41 | 65,721360 |
| 10 | 15,562306 | 26 | 41,450850 | 42 | 67,339394 |
| 11 | 17,180340 | 27 | 43,068884 | 43 | 68,957428 |
| 12 | 18,798374 | 28 | 44,686918 | 44 | 70,575462 |
| 13 | 20,416408 | 29 | 46,304952 | 45 | 72,193496 |
| 14 | 22,034442 | 30 | 47,922986 | 46 | 73,811529 |
| 15 | 23,652476 | 31 | 49,541020 | 47 | 75,429563 |
| 16 | 25,270510 | 32 | 51,159054 | 48 | 77,047597 |
Insert those values by hand for every partial (I might edit the patch one day so that you can edit the series spacing with a single control) like this. Remember that Bitwig has a very large decimal accuracy, altough it will only show the first two always:
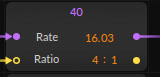
For rates above 32 you need to use the rate setting to create a multiplier. For example for partial number 40 the frequency is 64,103326 times the fundamental. You can set that value like this:
When all is done, we have a beautiful bell-like timbre that has a harmonic series that no acoustic instrument ever built has ever had. The reason why it sounds like a bell to us is that metal bells, bars, tubes and so on tend to have inharmonic spectra. They are an exception to the world of strings, wind instruments, human voice and so on, so our mind makes this connection based on our earlier empirical observations.
A further modification is to look at our tuning, and see if there’s some dissonance between the partials. With the new Micro-Pitch device we can change the semitone sizes so that possible problems are avoided. Also, since we are using an additive oscillator, we could either re-tune some of the partials, or remove offending partials altogether. The latter option will preserve the feel of an orderly series better.
However analysing these corrections, and what works best, is not straightforward. Now would be a good time to take a new look at the book by Sethares, where he will proceed through analysing this issue in great detail.
I certainly will, and I will get back to the issue later, when I have developed a workflow that makes sense. But for example’s sake, let’s check a few intervals to see how they line up. Since the tuning is not an equal temperament, the number of possible interactions between partials is very great. But I’ll show you the basic idea anyway:
Because of the principle of uncertainty, we can have either time or frequency accuracy when using a spectrum analyser (those peaks are probability functions actually, not discrete measurements, since we can’t sample-accurately measure the phase and frequency of a sinewave in a complex signal).
Let a long droning sound with the intervals you are interested in play, and tweak the tuning with a spectrum analyser window open until things start to line up more nicely. Set all modulations affecting the spectrum to zero, and open the filter fully. Here’s the first C D# G triad (never mind those quiter partials which are distortion, it was caused by one thing or other in the patch that I forgot to tune down) :
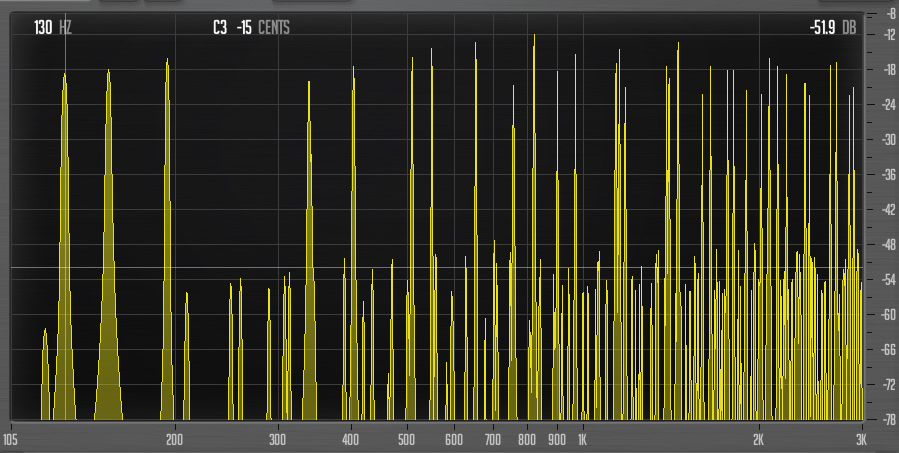
I will zoom in on that area where the partials seem to form clusters.
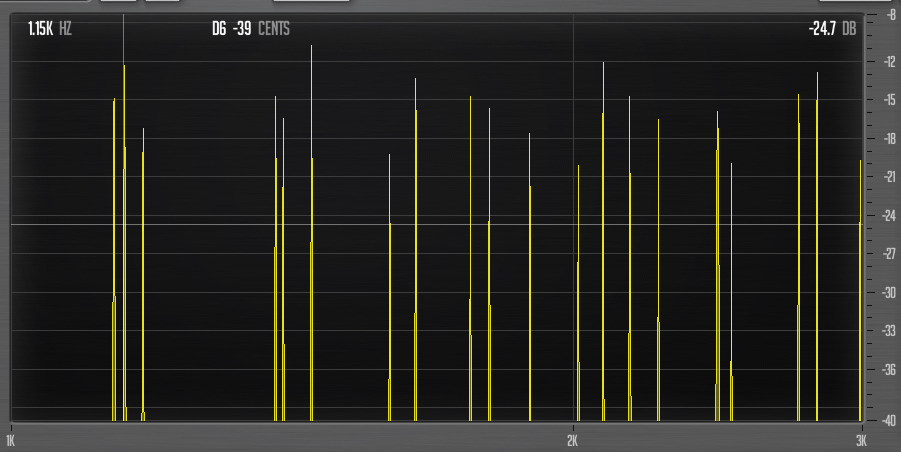
Now it’s a matter of keeping the analyser window open and adjusting either the tuning or the partials until you have something you like.
Listen carefully! Your ears are always the best judge!
Just for fun I brought down D# to 2.85 in Micro-Pitch. I also retuned several of the partials between 5 and 10. I ended up with this:
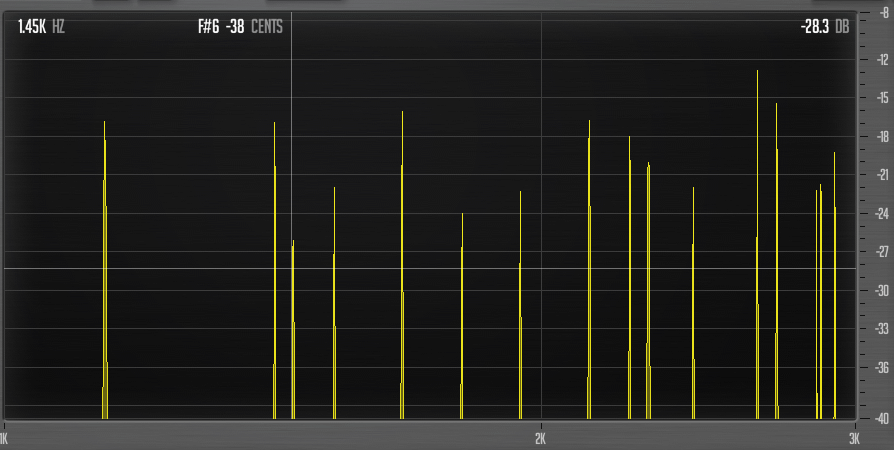
Let’s do a before-after for a DFA chord also. As it is:
After a bit of tuning:
I think the modified tuning sounds more pleasant and at rest. I only changed the tuning here, not any partials anymore, since I already changed them and I don’t want to deviate too far from the periodicity of the series.
There is a small trick here. With a window size of 16384 in Span, with which we can clearly tell apart the partials, the update speed of the analyser is quite slow. We can however change to a low resolution like 4096 for increased update speed. Now even though we can’t tell two closely partials visually apart, by observing the beating (volume modulation up and down) of the single peak around our frequency, we will know in which direction to tune. When the peak is more or less stable, we’re done. Afterwards you can check the details with maximum resolution when you don’t need to do live tweaks anymore.
Here you can see how the beating reveals (several!) mistuned partials even when a window size or 65535 in Manalyzer zoomed in on the area does not show the peaks separately.
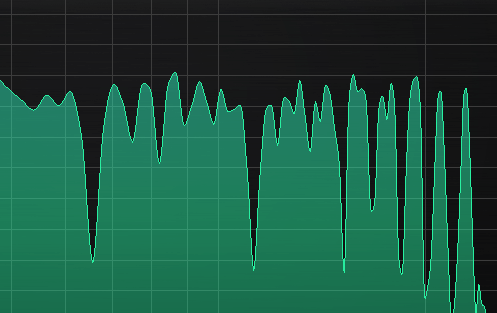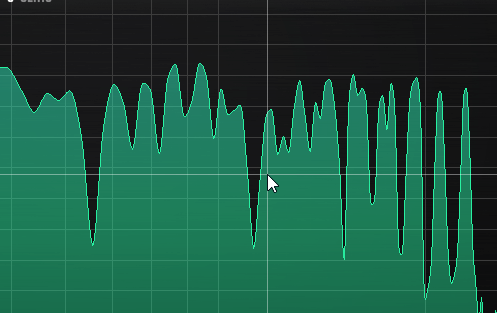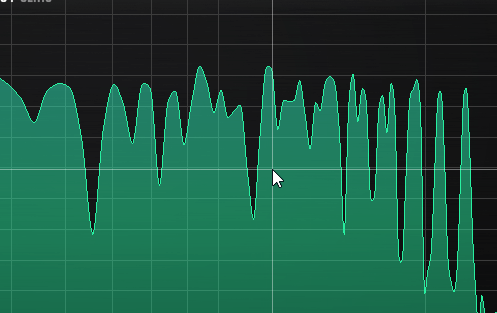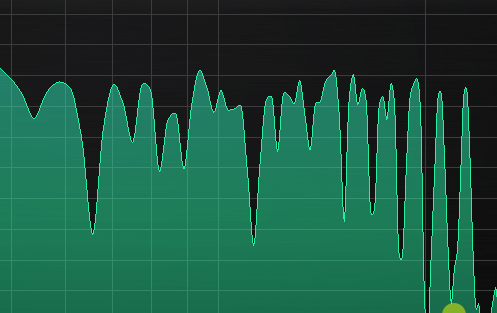
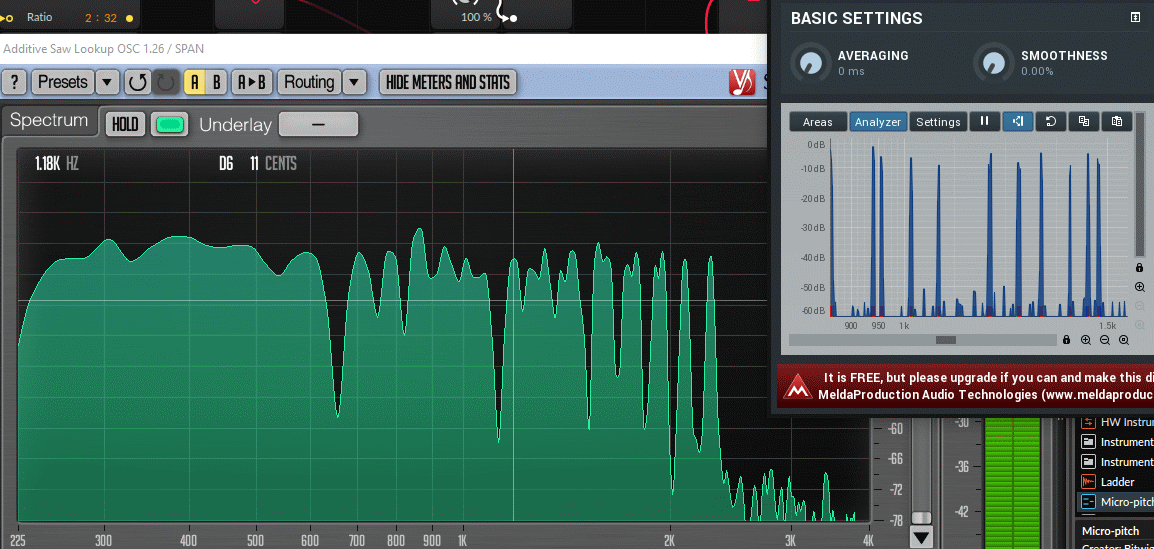
It’s a matter of taste how static the timbre should be. Slowish beating like shown here is not too bad in my opinion, but a lot of partials beating around 10-15hz can start to sound a bit chaotic, and faster than that can be outright dissonant.
Also, depending on the tuning, it might be very hard to make everything line up completely nicely. Live with that, drop some partials altogether, or change the tuning. Here is again the original sound clip, this time with the small adjustments I made.
I wasn’t thorough at all, since the actual tuning is such a complicated matter, and I want to re-read the book while thinking about how to best incorporate the ideas into a workflow within Bitwig.
And there you have it! Now you should be at least preliminarily prepared to embark upon the quest of mapping the last unknown frontier in music!
Download the project from here.
The website of William Sethares has a lot of useful information.
Also, the Facebook group Xenharmonic Alliance has a lot of very high quality discussion on the topic, along with the Tuning to Timbre Study Group.
